Num esforço para compreender como espécies diferentes coexistem, investigadores desenvolvem um modelo matemático que estabelece as interações inerentes à co-colonização como chave. O estudo, publicado na revista Bulletin of Mathematical Biology, liga a epidemiologia à ecologia e à evolução e propõe um novo modelo para a colonização de hospedeiros por espécies microbianas diferentes, um avanço fundamental para a análise de como diferentes espécies coexistem e para o entendimento da biodiversidade.

A forma como a biodiversidade é gerada e mantida são parte das questões mais centrais da ciência, cada vez mais importantes para a nossa qualidade de vida. Como podem espécies semelhantes coexistir num sistema? Quais dominam ou são excluídas? Sucumbirá o sistema à invasão por entidades externas? Podemos prever estas interações dinâmicas em sistemas com muitas espécies? Tipicamente, as simulações e a análise estatística são as abordagens escolhidas para responder a estas questões, mas as suas limitações levaram Erida Gjini, investigadora principal do Instituto Gulbenkian de Ciência, em colaboração com Sten Madec, da Universidade de Tours, em França, a usar a matemática para descobrir os princípios gerais que governam este tipo de sistemas.

Os dois investigadores usaram o sistema da transmissão de microrganismos entre hospedeiros como base do seu estudo teórico. Neste tipo de sistemas, cada espécie que coloniza o hospedeiro pode alterar o ambiente local e torná-lo propício ou não para a co-colonização por outra espécie. Se o ambiente melhora, o fenómeno é descrito como facilitação por pares; se piora, denomina-se competição entre pares. Este estudo propõe uma metodologia que explica o que ocorre numa rede com muitas destas interações em pares e como os seus membros engendram a sua coexistência.

“No início não sabíamos como as interações competitivas ou facilitadoras entre os vários membros se traduziriam em termos de dinâmica global do sistema. Lidávamos com muitas equações e o seu número aumentava quadraticamente com o número de espécies consideradas no nosso modelo. Por exemplo, para 10 espécies estudadas lidávamos com mais de 100 equações”, afirma Erida Gjini. O uso da técnica matemática da separação de escalas temporais foi muito vantajoso, já que esta permite separar as variáveis que mudam mais rápido das que mudam mais lentamente. 

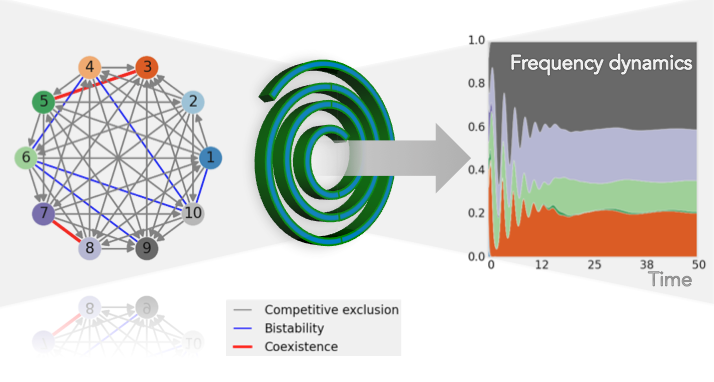
“Graças a esta técnica descobrimos uma equação simples que pertence à família das equações do replicador (muito usadas na teoria evolutiva dos jogos), que governa a dinâmica da frequência entre espécies no nosso modelo. Este tipo de equações consegue captar a essência da competição entre múltiplas estratégias num jogo com múltiplos jogadores e como o sucesso das mesmas muda ao longo do tempo. Surpreendentemente, descobrimo-la aqui, a partir da matriz de interações ‘sociais’”, explica Erida Gjini. Com estes resultados torna-se claro que as dinâmicas globais do sistema podem ser previstas inteiramente a partir do tipo e qualidade das interações em pares.

A um nível mais fundamental, a linguagem matemática deste trabalho realça que os organismos não vivem sós, mas são parte de uma rede de múltiplas relações de interdependência com outros, onde o sucesso individual depende das conexões próximas, mas também do contexto global”, revelam os autores. Este estudo traz vantagens a nível analítico e computacional para o estudo e interpretação de sistemas complexos com muitas dimensões, tanto no que toca à sua estabilidade como à sua evolução, estabelecendo assim a co-colonização como rota importante para a coexistência entre espécies e a biodiversidade.